Computational Modeling of Precipitation Kinetics in Superalloys

Authors: Stephane Forsik, Ning Zhou

Computational modeling of precipitation kinetics

Precipitation occurs when a supersaturated metallic solution becomes unstable and a new phase with a different composition and crystallographic structure nucleates and grows. The new precipitate often strains and strengthens the matrix via a critical strengthening mechanism called precipitation hardening (PH). For example, in Custom 465® (UNS S46500), a high-strength stainless steel, the precipitation of η-Ni3Ti in the martensitic matrix contributes to developing an ultimate tensile strength of 1720 MPa (250 ksi) at room temperature. In Waspaloy (UNS N07001), a nickel-base superalloy, the precipitation of Ni3(Al,Ti)-γ’ in the FCC matrix allows the superalloy to develop and maintain strength until 760°C (1400°F).

Thermodynamics is commonly used to calculate equilibrium compositions as a function of the chemistry and temperature, but does not capture the kinetic of precipitation reactions. Advanced kinetic approaches such as the Kampmann and Wagner numerical (KWN) model1 have been developed to calculate the growth, nucleation, and coarsening of a precipitate and have been implemented in commercial modeling programs such as Thermo-Calc®2, Pandat®3, or MatCalc®4. These are routinely used by the Carpenter Technology R&D team to simulate precipitation reactions and accelerate the development of new alloy compositions and processing parameters.

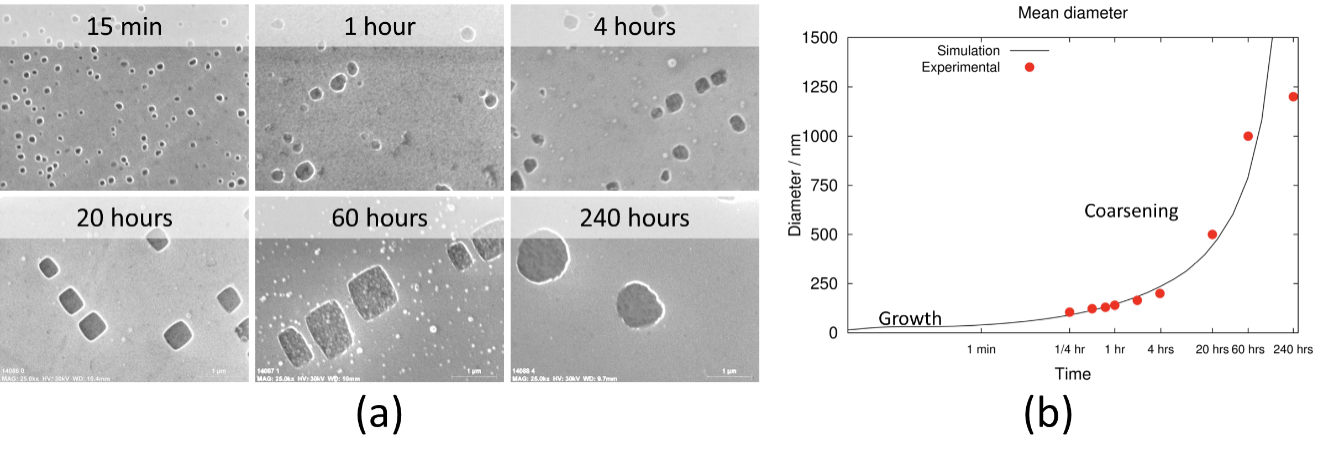
In the first example, a nickel-base superalloy was exposed to an aging heat treatment for 240 hours. Scanning electron microscopy (SEM) was performed at regular intervals (Figure 1a) and image analysis was used to measure the average γ’ diameter. Figure 1b shows the evolution of the measured γ’ diameter and the calculated γ’ diameter with time. Kinetic models are flexible, and critical kinetic parameters such the γ/γ’ interfacial energy or the density of nucleation sites in the matrix have to be fitted to the experimental data. Once a good match is obtained and the model is validated, it can be used to rapidly estimate the effect of changes in composition or temperature on the kinetic of precipitation without the need to conduct numerous experimental heat treatments or perform extensive characterization work.

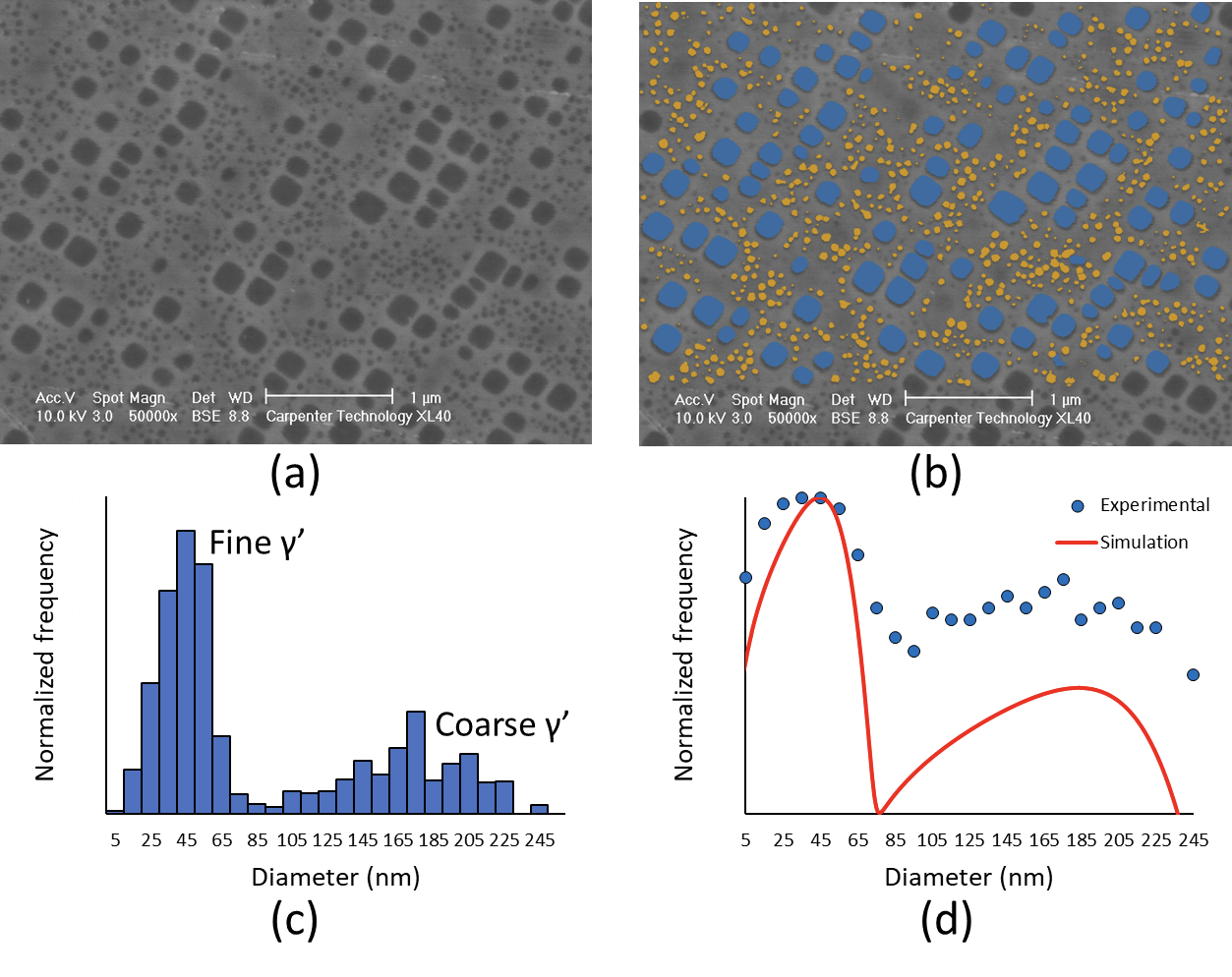
In the second example (Figure 2), a kinetic model was used to calculate the bimodal distribution of γ’ precipitates in a nickel-base superalloy after a 2-step aging heat treatment. The microstructure is composed of two different distributions of coarse and fine γ’ precipitates embedded in a γ matrix (Figure 2a), and image analysis was used to characterize the two populations (Figure 2b). The analysis was repeated on several SEM micrographs, and the particle size distribution was plotted in Figure 2c. The kinetic model was used to simulate the nucleation and growth of γ’ during aging and calculate the particle size distribution at the end of the heat treatment. The experimental and calculated particle size distribution are plotted on the same chart (Figure 2d), and show that the model captured the bimodal aspect of the distribution.

It is important to note that in this case, the model did not require any fitting and only used experimental kinetic parameters commonly reported in the literature; for example, 0.023 J⸱m-2 for the γ/γ’ interfacial energy.5 It also correctly predicted the average diameter of the fine γ’ precipitates (40 µm) and the coarse γ’ precipitates (~ 190 µm). The model can be used to further optimize the heat treatment, obtain the ideal γ’ precipitate distribution, and reach the desired mechanical properties.

These two examples show that thermodynamic and kinetic models can capture the fundamental mechanisms of precipitation reactions. Combined with various other solidification and deformation simulation software, the modeling tools allow R&D metallurgists at Carpenter Technology to rapidly assess new compositions and heat treatments, and considerably accelerate the design of new alloys and development of processing parameters.

Have questions? Get in touch with the experts at Carpenter Technology.